量子テレポーテーション

$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$
テレポーテーションといっても、人が瞬間移動するような現象ではありませんが、量子コンピュータの基礎である量子回路を学ぶには最もよい教材だと思います。なぜかというと、この回路は量子回路の基本中の基本である、アダマールゲート、制御NOTゲート、パウリゲートが含まれているからです。量子テレポーテーションは、EPRペアを用いて実現するのですが、これは後に式で示すようにアダマールゲートと制御NOTゲートで実現します。
この回路を理解すれば、少し量子回路がわかったような気になるお得な回路と言えると思います。
さて、古典計算機（今、我々が使っている普通のコンピュータ）はデータを読み出してコピーを容易に行えますが、量子計算機の情報はこのような操作ができません。
なぜかというと量子計算機で読み出すという操作は、対象を「観測」することで観測方法に依存した固有状態に遷移（波束の収縮）してしまい、読み出す前の状態が完全に決められなくなるからです。つまり答えを見るために行う「観測」という行為そのものが状態を変えてしまうということになります。
このように量子情報のコピーが作れないことを「量子クローニングの不可能性」といいます。つまりこれは、量子情報を伝送する途中で、誰かが密かに覗き見することが不可能であることを意味しています。しかし、量子情報を読み出すことができなくても、EPRペアを使うと遠隔地に伝達することが可能となります。これが量子テレポテーションです。
量子テレポーテーションは量子回路の基本なので、実験にもよく使われます。例えば東大の古澤先生が2004年に行った３者間の量子テレポーテーション実験、中国が2017年に行った地上と宇宙間の量子テレポーテーションなどがあります。

では、実際の量子テレポーテーション回路の説明に入ります。
図は、情報の送り手A（アリス）から受け手B（ボブ）に、1量子ビットの情報 \(\ket{\psi}\) を送るための量子回路です。
量子クローニングの不可能性によって、アリスは自分が持っている情報を読んで、その内容をボブに送ることはできないのですが、この量子演算回路によるとアリスが持っていた情報を、そのままボブに送ることが可能となります。

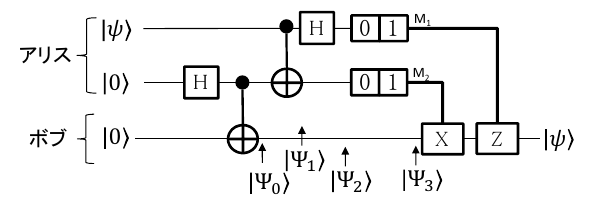
図の回路の状態\(\ket{\Psi_0}\)から\(\ket{\Psi_3}\)を順次計算します。
アリスの上から1ビット目の\(\ket{\psi} = c_0\ket{0}+c_1\ket{1}\)が、ボブに送りたい情報です。
\(c_0とc_1\)は任意の複素数で、\(\ket{0}と\ket{1}\)それぞれにそれらの複素数を掛けて加えた重ね合わせ状態を示します。つまり\(c_0とc_1\)が送りたい情報そのものと言えます。この情報が伝達されると、\(\ket{\psi}\)をそのまま受け取ることになり、それを観測すると\(c_0およびc_1\)の絶対値の確率で\(\ket{0}または\ket{1}\)が得られることになるのです。
アリスの\(\ket{0}\)はアダマールゲートを通ると\(\ket{0}+\ket{1}\)となり、ボブの入力と共にコントロールNOTゲートを通過すると以下の式になる。つまりアリスとボブの間にEPRペアができることになります。
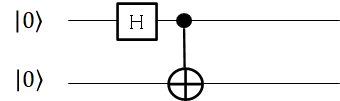
先に量子エンタングルメント（量子もつれ）の説明をします。２つの粒子が量子的にもつれあった状態になっていると、片方の粒子の状態が決まると、もう一方の粒子の状態が決まるという不思議な状態になります。この量子もつれ状態にある粒子のペアをEPRペアと言います（EPRは3人の物理学者の頭文字で、Eはアインシュタイン）。この量子もつれ状態は例えば次の図のようなアダマールゲートとコントロールNOTゲートを用いてつくることができます。
入力は量子ビットの上から順に並べて、\(\ket{0}\otimes\ket{0}\)です。\(\otimes\)を挟んだビットはそれぞれ独立したビットという意味ですが、いちいち面倒なので、通常は\(\ket{00}\)と記載します。上位のビットがアダマールゲートを通過すると\(\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{0}\)となります。
その後にコントロールNOTゲートを通過すると、1ビット目が\(\ket{0}\)の場合は2ビット目はそのまま通過するので、\(\ket{0}\)となり、1ビット目が\(\ket{1}\)の場合は2ビット目は反転するので、\(\ket{1}\)となりますので、最終的な出力は\(\frac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \)となるわけです。これを見ると1ビット目が決まると2ビットが自動的に決まる、つまりもつれあった状態をつくることができることがわかります。

では、再び図1の量子テレポーテーション回路に戻ります。
\(\ \ \ \ket{\Psi_0} = \ket{\psi} \otimes \frac{1}{\sqrt{2}}(\ket{00}+\ket{11}) \)
次にアリスからの情報\(\ket{\psi}\)と上記の出力がコントロールNOTゲートを通過すると、
\(\ \ \ \ket{\Psi_1} = \frac{1}{\sqrt{2}} \{c_0 \ket{0}\otimes(\ket{00}+\ket{11}) + c_1 \ket{1}\otimes(\ket{10}+\ket{01} \} \)
さらにアダマールゲートを通過すると、
\(\ \ \ \ket{\Psi_2} = \frac{1}{2} \{c_0 (\ket{0}+\ket{1})\otimes(\ket{00}+\ket{11}) + c_1 (\ket{0}-\ket{1})\otimes(\ket{10}+\ket{01} \} \)
これを上位2ビットが同じものを括りだして整理すると、
\(\ \ \ \ket{\Psi_2} = \frac{1}{2} \{ \ket{00}\otimes(c_0\ket{0}+c_1\ket{1}) + \ket{01}\otimes(c_0\ket{1}+c_1\ket{0}) + \ket{10}\otimes(c_0\ket{0}-c_1\ket{1})+\ket{11}\otimes(c_0\ket{1}-c_1\ket{0}) \} \)
\(\Psi_2\)のあとで、アリスは検出器M1とM2を用いて古典的な測定を行います。
\(\Psi_2\)の式の通り、各ビットの絡み合いは解けており、M1とM2の測定値に対応して、それぞれボブの異なる量子ビット状態\(\Psi_3\)に対応することになります。
M1とM2の測定値に対応した、適当な1ビットユニタリ演算（パウリゲート）を施すことで、\(\ket{\psi}\)を復元できることになります。

\(\ \ \ M1,M2\hspace{20mm} \Psi_3 \hspace{30mm} パウリゲート通過後 \)
\(\ \ \ 00 \ \ \ \longrightarrow\ \ \ c_0\ket{0}+c_1\ket{1} \ \ \ \longrightarrow\ \ \ c_0\ket{0}+c_1\ket{1}　（何もしない） \ \)
\(\ \ \ 01 \ \ \ \longrightarrow\ \ \ c_0\ket{1}+c_1\ket{0} \ \ \ \longrightarrow\ \ \ c_0\ket{0}+c_1\ket{1}　（\fbox{X}を作用） \ \)
\(\ \ \ 10 \ \ \ \longrightarrow\ \ \ c_0\ket{0}-c_1\ket{1} \ \ \ \longrightarrow\ \ \ c_0\ket{0}+c_1\ket{1}　（\fbox{Z}を作用） \ \)
\(\ \ \ 11 \ \ \ \longrightarrow\ \ \ c_0\ket{1}-c_1\ket{0} \ \ \ \longrightarrow\ \ \ c_0\ket{0}+c_1\ket{1}　（\fbox{X}+\fbox{Z}を作用） \)
つまりそのままアリスの情報がボブに伝えられたことになります。
EPRペアを使っているので、情報を光速を超えて送ることができるように見えますがそうではありません。図1を見ればわかるように、アリスの情報をボブが読み出すためには、1ビット目と2ビット目を測定した古典情報（M1、M2）を、「古典的に」送る必要があります。結局、光速を超えた情報伝達はできず、相対論を超えるような情報伝達はできないことになります。。