ネイピア数 e
数年前に、ある人権団体の会合で、あなたは理系だから数学の\(\ e\ \)について話をしてほしいと言われ、作成した資料です。ほとんどが文系の方だったのですが、皆さん、??という顔をされていました。私の説明(熱意?)が不足していたのかな…。
ネイピア数\(\ e\ \)とは?
・数学(科学、工学など含む)で使用される基本的な数字
・オイラー数、自然対数の底などとも呼ばれる
・無理数であり、超越数である。
無理数:整数の比で表せない数
超越数:無理数のうち、有理数の係数をもつ代数方程式の解とならない数
・値は、2.718281828459014.……
(記憶方法の例:フナ一羽二羽一羽二羽しごくおおいよ)
ところで…話は変わりますが、利息の計算をします。
100万円を預けて、利息が1年で100%(!)とします。
1年後はいくらになるか?
①そのままだと 100万円+利息100万円=200万円
②半年ごとに50%ずつ利息がつくと(半年複利)
(100万円×1.5)×1.5=225万円
③3か月ごとに25%ずつ利息がつくと(3か月複利)
(100万円×1.25)×1.25×1.25×1.25=約244万円
利息がつく期間をどんどん短くしていくと(1秒毎とか)どうなるでしょう?
①どこかで逆転して減っていく
②どんどん増えていく
③ある一定の値に近づく
答えは…③ある一定の値に近づいていきます。
約271万8281円 ⇒ 増加率2.71828(これがネイピア数e!)
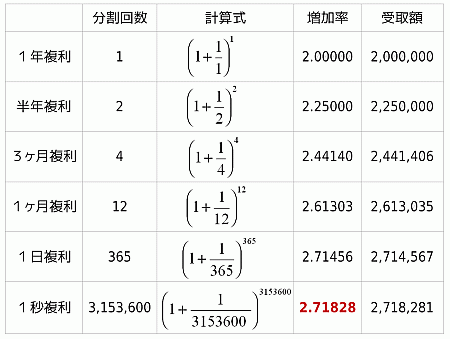
①利息のつく期間を限りなく短くしていくとお金の増加率は
以下の式になります。
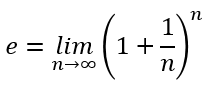
例えば関数電卓でn=1000などとして、1.001の1000乗を計算してみて下さい。桁を上げるとネイピア数に近づいていきます。
オイラーの等式
世の中で最も美しい式と言われています
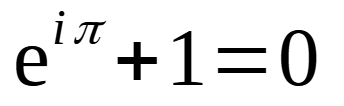
\(e\) : ネイピア数(超越数)
\(i\) : 虚数、すなわち2乗すると −1 となる数
\(π\) : 円周率、すなわち円の周の直径に対する比率(超越数)
実に感動的で美しい公式です。
『博士の愛した公式』小川洋子著 より 抜粋 1)
果ての果てまで循環する数と、決して正体を見せない虚ろな数が、簡潔な軌道を描き、一点に着地する。どこにも円は登場しないのに、予期せぬ宇宙から\(\pi\)が \(e\) の元に舞い下り、恥ずかしがり屋の \(i\) と握手をする。彼らは身を寄せ合い、じっと息をひそめているのだが 一人の人間が1つだけ足し算をした途端、何の前触れもなく世界が転換する。すべてが\(0\)に抱き留められる。オイラーの公式は暗闇に光る一筋の流星だった。暗黒の洞窟に刻まれた一行の詩だった。
『ファインマン物理学Ⅰ 力学』より 6)
物理学で著名なファインマン教授は、オイラーの公式は、「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」であると述べています。
Richard Feynman called Euler’s formula “our jewel” and “one of the most remarkable, almost astounding, formulas in all of mathematics.”
<参考・引用文献>
1)『博士の愛した公式』小川洋子 新潮文庫、 映画『博士の愛した公式』

中学教師役の吉岡秀隆が生徒にオイラーの公式を語る場面が見ものです。
2)『数学 想像力の科学』瀬山士郎 岩波科学ライブラリー
気軽に読めます。
3)『オイラーの公式がわかる 数学の至宝を知る』原岡喜重 講談社ブルーバックス
オイラーの公式の導き方、応用を分かりやすく説明してくれます。
4)『オイラーの贈物 人類の至宝 \(e^{iπ}=-1\ \)を学ぶ』吉田武 ちくま文芸文庫

少し本格的に復習や勉強したい場合は、これが良いと思います。
5)『高校数学でわかるフーリエ変換―フーリエ級数からラプラス変換まで』竹内淳 ブルーバックス
もう少し視野を広げてフーリエ変換まで勉強するのはこれが良いかと思います。世界の見え方が変わります。
6)『ファインマン物理学Ⅰ 力学』 坪井忠二訳 岩波書店

ファインマン教授の名著で、物理学を本格的に学ぶためのシリーズの第1巻。オイラーの公式について、「これは我々の至宝である」と述べています。