素数と暗号
$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$
<素数の話>
素数は不思議な魅力があるせいか、一般書から専門書まで素数を扱った本がいっぱいあります。
あまりに難しいので深いところまでは手が届かないのですが、ある人権団体の集まりで素数と暗号について話す機会があり、そのために少し齧った内容を紹介します。
素数(prime number)とは
自然数(1,2,3,4・・・・)のうち、1と自分自身でしか割り切れない数。(但し、1は含まない) これはほとんど誰でも知っていますよね。
それだけの数字なのに、素数について今もわからない問題がいくつもあります。例えば、
●ゴールドバッハ予想
あらゆる偶数は二つの素数の和で表されるという予想
4=2+2 6=3+3 8=3+5 10=3+7=5+5 ・・・・何となくいけそうな感じですが、ずっと成り立つのかは未解決。
4000000000000000000(0が18個)まで確かめられているそうです。
●双子素数は無限にあるか?
双子素数とは、差が2の素数の組のことですが、これが無限に存在するかどうかは未解決の問題。
双子素数の例)3と5、11と13、41と43
素数はこんなところにも出てきます。
●素数ゼミ
13年や17年といった素数年ごとに大量発生する有名なセミです。羽化する年の最小公倍数が小さいと交雑が起こって羽化する年がバラバラになりますが、素数年どうしだと交雑が起こるまでの年数が大きくなり、生き残るために大量発生することができるそうです。
●宇宙の構造と関わっている?
素数の分布が原子構造と関わっている例があるそうです。なぜかはわからないそうです。
素数についての基本的な知識
●素数を計算する式は存在しない。つまり素数を計算で出せないということです。
●素数は無限に存在します。
背理法で証明できます。素数が有限個で、最大の素数がPと仮定します。
素数を小さいものから順にPまで掛けて、1を足してQとすると
Q=2×3×5×7×11×・・・・・・・×P+1
Qは1とQでしか割り切れないからPより大きい素数となり矛盾します。
従って、素数が有限である仮定が間違っていることになりますので、無限に存在するということになります。
素数の分布について
●全ての素数の逆数の和は?
$$\hspace{10pt} \frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+……=∞ $$
となり、素数の逆数の和は無限大に「発散」します。これからも素数は無限に存在することがいえます。
●全ての双子素数の和は?
差が2の素数を双子素数といいます。つまりこのような組み合わせです
(3,5) (5,7) (11,13) ……
双子素数は無限にあるかどうか現在も未解決です。しかし、双子素数の逆数の和は収束することが分かっています。
$$\hspace{10pt} \left(\frac{1}{3}+\frac{1}{5}\right)+\left(\frac{1}{5}+\frac{1}{7}\right)+\left(\frac{1}{11}+\frac{1}{13}\right)+…\ =\ 1.90216…… $$
逆数の和が収束するのにも関わらず、双子素数が無限にあるか有限にあるかわからないのです。実に不思議です。
●オイラー積
この式!素晴らしいです!この式を見たときは本当に感動しました。最初は何でこんな式が成り立つの?という感じでしたが…
$$\hspace{10pt} \sum_{n=1}^{∞}\frac{1}{n^s} \ =\ \prod_{p}\frac{1}{1-\frac{1}{p^s}} \ \ \ \left( pは素数 \right) $$
これをよくよく見ると何となく成り立つような気がしますよね?!
$$\hspace{10pt} \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+… \ =\ \left(\frac{1}{1-\frac{1}{2^s}}\right)\left(\frac{1}{1-\frac{1}{3^s}}\right)\left(\frac{1}{1-\frac{1}{5^s}}\right)\left(\frac{1}{1-\frac{1}{7^s}}\right)… $$
この式の左辺はゼータ関数と呼ばれる関数で素数の研究で非常に重要な関数です。
$$\hspace{10pt}\zeta{(s)}\ = \ \sum_{n=1}^{∞}\frac{1}{n^s} $$
●リーマン予想
ドイツの数学者リーマンが1859年に提示した予想で、約150年の間、今も未解決の大難問です。ではリーマン予想とはどのような問題でしょうか?
ゼータ関数
$$\hspace{10pt}\zeta{(s)}\ = \ \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+… \ \ \ s:複素数 $$
の値が0になる解は、全て複素数の実数部分が1/2である。但し、トリビアル(当たり前)な解(sが負の偶数)を除く。
たった、それだけだそうです。では、これが解決したらどうなるのでしょうか?なんと素数の分布が解明されるそうです!
●素数の分布について
0から整数xまでの間にある素数の個数を\( \pi (x)\)とすると、
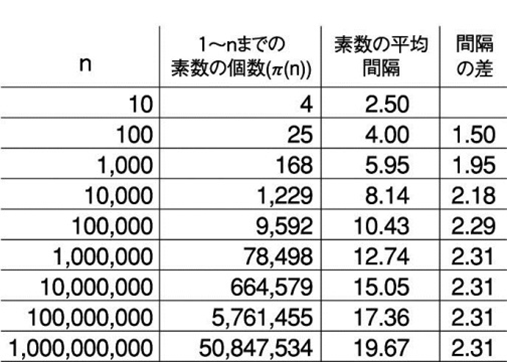
①つぎの式はガウスの素数公式として知られています。
$$\hspace{10pt} \pi (x) \ \simeq \ \frac{x}{\ln x} $$
②つぎの式もガウスの素数公式として知られています。
$$\hspace{10pt} Li (x) \ \simeq \ \int_2^x\frac{dt}{\ln t} $$
③これはリーマンの素数公式
$$\hspace{10pt} R(x)\ = \ Li(x)-\frac{1}{2}Li(x^{\frac{1}{2}}) -\frac{1}{3}Li(x^{\frac{1}{3}}) -…$$
④これもリーマンの素数公式
$$\hspace{10pt} R(x)\ = \ 1+ \sum_{k=1}^{∞}\frac{(\ln x)^k}{kk!\zeta{(k+1)}} $$
⑤最後にこれがリーマンの究極の素数公式だそうです。
$$\hspace{10pt} \pi(x) \ =\ R(x) \ -\ \sum_{\rho}{}R(x^\rho) \ \ \ \ \ \ ※\rho :ゼータ関数の零点$$
リーマン予想が解決すると、ゼータ関数の零点の性質がわかるので、素数分布\(\pi(x)\)が再現できることになるそうです。
何という素晴らしいことでしょう!リーマン予想の証明で素数の分布が解明される?リーマン予想自体に宇宙に潜む未知の法則が隠されているかもしれないという数学者もいるそうなので、すごく楽しみです。
<素数と暗号>
暗号は大昔から秘密の情報を共有したい相手に、別の人に情報が洩れないように伝えるため様々な工夫がされてきました。
従来から良く用いられてきたのは、文字と文字を変換する表を送り手と受け手が共有し、元の文を変換する方法です。
この文字と文字を変換する表を鍵と考えると、送り手と受け手のみが秘密の鍵を持っていれば暗号として成り立つということなります。
但し、この変換表が単純な表だと、すぐに解読されてしまうし、そもそもその鍵の受け渡しをどのように行うのかなど色々と問題があって、この方式だと経済的な取引に使うのは危険極まりないことになると思われます。
ここで考え出されたのが暗号方式の一つがRSA暗号と呼ばれる公開鍵暗号です。情報を受ける人は、公開鍵と秘密鍵の2つを準備します。公開鍵は情報に鍵をかけて暗号化するための鍵で、鍵自体は公開します。秘密鍵は暗号化された情報を復元するための鍵で、受け手の人は自分以外の人には決して漏らしてはなりません。
なぜこのようなことができるのか?この鍵に素数を用いるのです。
桁の大きい2つの素数を掛け合わせた数字があるとします。その掛け合わせた数字しか知らない場合に、掛け合わせる前の二つの素数を知る(つまりは素因数分解する)ためには膨大な時間がかかります。基本的には、小さい素数から順に割っていって割り切れる数字を探すしかないからです。現在鍵として用いられている2048 bit(二進数で2048桁、十進数で617桁)の数字を2つの素数に分解するためにはスーパーコンピューターを用いても何億年もかかります。単なる数字の積の計算なので、計算できないということでは無く、現実的な時間では計算できないということなのです。とはいうものの計算が効率的に行われるアルゴリズムや計算速度が速くなる計算機が出てくると、話が変わることになります。また量子コンピュータのような計算機が実現できればこのような計算も容易になるかもしれません。
それではRSA暗号について簡略化して述べます。詳しくは専門書等を参照して下さい。
まず、互いに異なる(大きな)素数\(p,q\)を選びます。次の順序で鍵を生成します。
\(\hspace{10pt}①\ n\ =\ pq\ \)を計算します。
\(\hspace{10pt}②\ \Phi(n)\ =\ (p-1)(q-1)\ \)を計算します。
\(\hspace{10pt}③\ \Phi(n)\ \)と素な整数\(\ e\ \)をランダムに選びます。
\(\hspace{10pt}④\ ed\ \equiv\ 1(mod\ \Phi)\ \)となる整数\(\ d\ \)を求めます。
以上から
$$\hspace{10pt} n,e:公開鍵、\ \ \ \ \ d:秘密鍵$$
が求まります。
暗号化と復号化は以下のように行います。
メッセージを数値化したもの\(\ m\ \)を、公開鍵\(\ n,e\ \)で暗号\(\ c\ \)を生成し、秘密鍵\(\ d\ \)で復号化します。
1.暗号化
\(\hspace{10pt}c\ \equiv\ m^e(mod\ n) \)
つまり、\(m\)の \(e\)乗を\(n\)で割った余りが暗号\(c\)となります。
2.復号化
\(\hspace{10pt}m\ \equiv\ c^d(mod\ n) \)
つまり、\(c\)の \(d\)乗を\(n\)で割った余りがもとのメッセージ\(m\)となります。
<参考・引用>
1) 『素数はなぜ人を惹きつけるのか』竹内薫 朝日新書
素数の入門書として最適。素数ゼミの話から、素数が宇宙の構造とつながっている?など面白い話がわかりやすく書いています。
素数の公式などはほとんどこの本を参考にさせて頂きました。素数に興味を持つ人は是非お読み下さい!

2) 『素数の音楽』マーカス デュ・ソートイ 新潮文庫
今だ未解決の難問「リーマン予想」に挑む天才たちを描くノンフィクション。啓蒙書としては一番のお勧め。

3) 『ジェノサイド』上・下 高野和明 角川文庫
人智をはるかに超える知性を備えた新人類の出現が「人類の危機」をもたらす?この新人類は公開鍵暗号方式(RSA)も難なく解いていしまう。ドキドキしながら一気に読めるエンターテイメント作品。めちゃめちゃ面白いです。

4) 『なるほどナットク!暗号がわかる本』イオタゼミ オーム社
暗号の基礎知識を学ぶための入門書として最適。

5) 映画『イミテーション・ゲーム/エニグマと天才数学者の秘密』
コンピューターの概念を初めて理論化し、エニグマの暗号解読により対独戦争を勝利に導いたアラン・チューリング。その激動の人生を描いた映画

6)『量子コンピューターが本当にすごい』 竹内薫 PHP新書
スーパーコンピュータを遥かに凌ぐ計算能力を持つ量子コンピュータが暗号も解いてしまう?量子コンピュータが社会をすっかり変えてしまうかも。量子コンピュータに興味のある方は是非お読み下さい!
