量子コンピュータによるシミュレーション


$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$
量子コンピュータのシミュレーションのライブラリがいくつか公開されています。以下、この文章は2019年に書いたので少し古いかもしれません。例えば2016年にIBMはクラウド環境IBM Quantum Experienceの提供を開始しました。GUIで音符を並べるように量子ゲートを配置したり、後に述べるPython言語で量子ゲート回路を記述する方法で、PC上でシミュレーションを実行することができます。また、米国のIBMワトソン研究所の量子コンピュータを利用した実験も可能です。
かといって、もちろん現段階では汎用となりうる量子コンピュータがあるわけではないので、大規模な回路のシミュレーションはできません。規模はともかく、ある程度の回路をPC上でシミュレーションを実施することにより、量子計算の動作原理の理解に役立つと思います。ここでは、書籍[中山茂, Qiskit量子プログラミング入門, 2019]を参考にして、IBMのQiskitを用いて、Python言語によるプログラムを作成し、シミュレーションと実機による実験を行ってみました。

QiskitはIBMが2017年に公開した量子情報ソフトウェアキットです。Webブラウザ上で、Python言語でプログラミングすることでPC上のシミュレーションや、IBMの量子コンピュータでのクラウド量子計算を実行することができます。またPythonを使用することで、膨大なライブラリを利用した古典的な計算と、量子コンピュータによる計算との組み合わせることができるそうです。
今回はQiskitを用いて、量子テレポーテーションの簡略化した量子回路モデルによりシミュレーション及び、実機による実験を行ってみました。
図１が実験に用いた量子回路です。別に説明した量子テレポーテーションの量子回路と異なり、AliceからBobの送る古典情報の部分を省略した簡易的な実験となります。（古典情報部分が制御パウリZゲートのみになっています。制御パウリZゲートは、制御側が\(\ket{0}\)の場合はそのまま通過し、\(\ket{1}\)の場合はパウリZ変換されるゲートです。パウリZゲートは「基本的な量子ゲート」を参照してください。）

図１．量子テレポーテーション実験回路

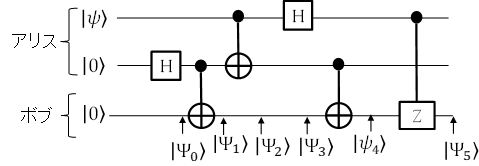
AliceがBobに送る情報を\(\ket{\psi} = c_0\ket{0}+c_1\ket{1}\)とすると、図1の\(\ket{\Psi_0}\)から\(\ket{\Psi_5}\)の状態は以下の式で表されます。
\(\hspace{10pt}\ket{\Psi_0} = (c_0\ket{0}+c_1\ket{1})\otimes\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{0}\)

\(\hspace{10pt}\ket{\Psi_1} = (c_0\ket{0}+c_1\ket{1})\otimes\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})\)

\(\hspace{10pt}\ket{\Psi_2} = \frac{1}{\sqrt{2}} \{ c_0\ket{0}\otimes(\ket{00}+\ket{11})+c_1\ket{1}\otimes(\ket{10}+\ket{01})\}\)

\(\hspace{10pt}\ket{\Psi_3} = \frac{1}{2} \{ c_0(\ket{0}+\ket{1})\otimes(\ket{00}+\ket{11})+c_1(\ket{0}+\ket{1})\otimes(\ket{10}+\ket{01})\}\)

\(\hspace{10pt}\ket{\Psi_4} = \frac{1}{2} \{ c_0(\ket{0}+\ket{1})\otimes(\ket{00}+\ket{10})+c_1(\ket{0}+\ket{1})\otimes(\ket{11}+\ket{01})\}\)

\(\hspace{10pt}\ket{\Psi_5} = \frac{1}{2} \{ c_0(\ket{000}+\ket{010}+\ket{100}+\ket{110})+c_1(\ket{011}+\ket{001}+\ket{111}+\ket{101})\}\)

\(\hspace{20pt}=\frac{1}{2} \{ c_0(\ket{00}+\ket{01}+\ket{10}+\ket{11})\otimes\ket{0}+c_1(\ket{01}+\ket{00}+\ket{11}+\ket{10})\otimes\ket{1}\}\)

\(\hspace{20pt}=\frac{1}{2} \{ (\ket{00}+\ket{01}+\ket{10}+\ket{11})\otimes(c_0\ket{0}+c_1\ket{1})\}\)
従って、この量子回路を動作させると、BobはAliceの入力情報を受け取ることになります。
Aliceの情報がBobに送られていることを確認するために、|0⟩と|1⟩の重ね合わせの比率を変更して実験をしてみました。
以下のユニタリ回転ゲート \(U_3 (θ,ϕ,λ)\)を用いて、
$$\hspace{10pt}U_3 = \left[\begin{array}{cc}\cos{(\frac{\theta}{2})} & -e^{i\lambda}\sin{(\frac{\theta}{2})} \\-e^{i\phi}\sin{(\frac{\theta}{2})} & e^{i(\lambda+\phi)}\cos{(\frac{\theta}{2})} \end{array}\right]$$
\( \lambda=0,\phi=0\)とすると、\(\ket{0}\)は\(U_3\)により
$$\hspace{10pt}U_3\ket{0} = \left[\begin{array}{cc}\cos{(\frac{\theta}{2})} & -\sin{(\frac{\theta}{2})} \\ \sin{(\frac{\theta}{2})} & \cos{(\frac{\theta}{2})}\end{array}\right] \left[\begin{array}{c}1 \\ 0 \end{array}\right] = \cos\left(\frac{\theta}{2}\right)\ket{0}+\sin\left(\frac{\theta}{2}\right)\ket{1}$$
と変換されます。
つまり、Aliceの情報\(\psi\)を\(\cos\left(\frac{\theta}{2}\right)\ket{0}+\sin\left(\frac{\theta}{2}\right)\ket{1}\)とし、\(\theta = \frac{\pi}{k}\)の\(k\)を\(k=1,2,3,4,5\)と振り、図２のようにブロッホ球面内で送る情報を変化させました。

図３．実験で用いたAliceの情報

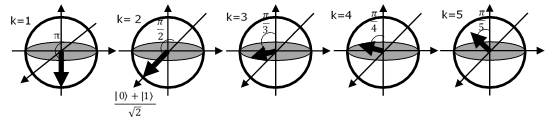
Aliceの情報がbobにテレポートされた場合、Bob受け取った情報を測定すると、\(\ket{0}\)の確率は\(\cos^2\left(\frac{\pi}{2k}\right)\)、\(\ket{1}\)の確率は\(\sin^2\left(\frac{\pi}{2k}\right)\)になるはずです。

まずは実機ではなくシミュレーションをしてみることにします。実験の回路は図１の回路のAliceの情報を、先ほど述べた入力に変更するために、図４のようにユニタリ演算を行う\(U_3\)ゲートに変更しました。

図４．実験用の量子テレポーテーション回路

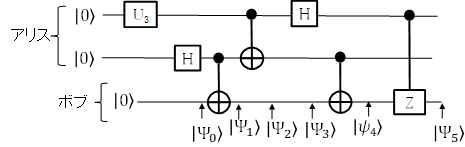
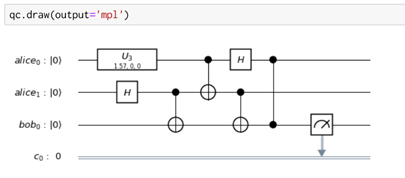
この量子回路をpythonで記述すると図５のようになります。
最後から4行目に「qasm_simulator」と指定することで、pythonによるシミュレーションが実行されます。

図５．Pythonによるシミュレーションプログラム

ｋ＝１から5まで、それぞれ1024回繰り返しを行ってみました。実行結果は以下のように表示されます。

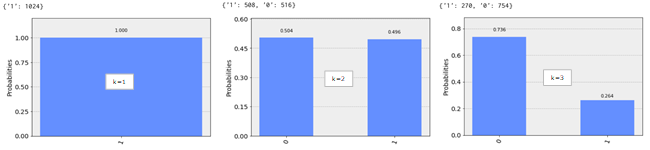
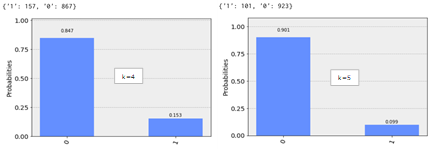
この結果をまとめると、aliceの送付情報とbobの受信情報が完全ではありませんが、ほぼ一致していることがわかります。

表１．Pythonによるシミュレーション結果

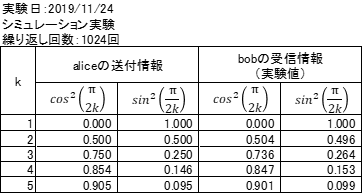
次にIBMの量子コンピュータの実機実験を行ってみました。IBMが提供するQiskit SDKをインストールし、登録してTokenを入手することで、Python言語でIBMの量子コンピュータにアクセスすることができます。IBMの量子コンピュータのうち、５qbitを持つ「ibmq_5_yorktown」（2019年当時）を用いて、シミュレーションの場合と同様の実機による量子テレポーテーション実験を行いました。

IBMの量子コンピュータのハードウェアは下図のような構造になっています。（2019年のIBMのホームページより）

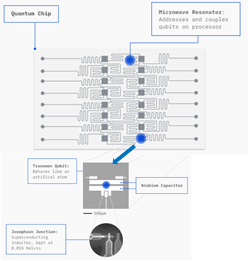
超伝導体の電極がジョセフソン接合を介して接続されており、電子ペアが2枚の電極のどちらにあるかで「0」と「1」が表現され、重ね合わせ状態をつくります。電極は窒化ニオブなどが用いられており、超電導チップ上にこの量子ビットが配置され、電極にはマイクロ波共振器が接続されており、外部から電気信号を入力することにより、量子ビットへの入力や読み出しを行うことができます。また量子ビット間を電気信号線を通じて接続し、相互作用させることができます。量子チップは超電導状態にするために15mK程度にまで冷却されているそうです。
Python言語での記述は図６のようになります。シミュレーション実験の場合の「qasm_simulator」の代わりに「ibmqx2」と指定することで、量子コンピュータによる計算が実行されます。

図６．Pythonによる量子コンピュータの実行プログラム

シミュレーション実験と同様にｋ＝１から5まで、それぞれ1000回繰り返しを行いました。実行結果は以下のように表示されました。

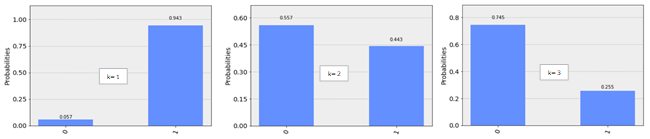
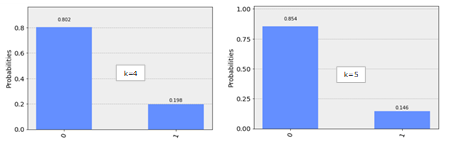
実験結果をまとめると表２のようになりました。Bobの受信情報はAliceの送付情報に近い値を得られましたが、シミュレーション実験の結果と比較すると差が大きいことがわかります。量子コンピュータ実機の方がノイズが多いことが確認されました。

表２．Pythonによるシミュレーション結果２

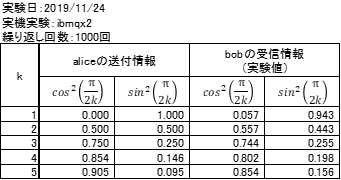
この実験にそれほどの意味があるかというと疑問ですし、答えがわかっている問題がそのまま出てきただけで、量子コンピュータのメリットを確認できるというわけではありませんが、量子コンピュータと、そのプログラミングに触れることができるという学習ツールとしての効果は大きいのではないかと思います。