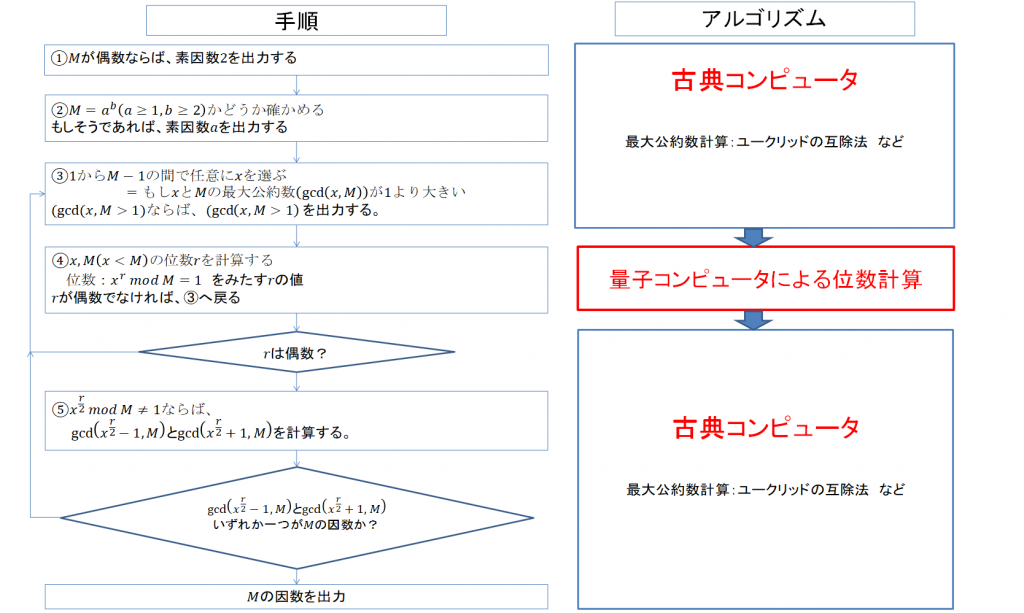
ショアのアルゴリズム

$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$

ショアのアルゴリズムとは、古典計算機では非現実的な時間がかかる大きな数の素因数分解を、量子コンピュータにより多項式時間で効率良く解くアルゴリズムです。大きな数の素因数分解を計算するためには、問題の大きさ（この場合は素因数分解をしたい整数の桁数）に対して指数関数的な時間がかかります。これに対して多項式時間というのは、問題の大きさの累乗程度で計算ができるということです。つまり問題が大きくなると圧倒的な差となります。このような問題を解くアルゴリズムとして1994 年にピーター・ショアが提案しました。現在広く用いられているRSA 暗号が解読される可能性があるということで、発表当時には世界中に大きな衝撃を与えた有名なアルゴリズムです。実際にはまだこのような計算を実行できるような量子コンピュータは存在しないので、今のところは解読される心配は不要で、RSA暗号は一般的な暗号方式として使われています。
図１に示すように、素因数分解の手順において、計算時間のかかる位数計算を量子計算機で行い、それ以外は古典計算機で計算することになるかと思われます。恐らく現在の古典コンピュータのような汎用コンピュータを実現するのはしばらくは難しいかと思いますので、実現するとしてもこのような形かと想像されます。
位数計算とは、２つの素数の積\(M\)を因数分解するにあたり、\(a\)は\(M\) に対して素な数とし、\(a\ mod\ M\)（\(a\)を\(M\)で割った余り） に関する位数、つまり、\(a^x\ mod\ M\) の周期\(r\) を求めることになります。位数計算は、量子離散フーリエ変換を用いるアルゴリズムにより高速に実行することができると言われています。

こう言ってしまえば簡単そうですが、ショアのアルゴリズムは素人にとっては非常に難解で、式の展開も2進表記も混じったりしてわかりにくいかと思います。大学院のテーマに量子コンピュータを選択したものの、なかなか分からないことも多く研究は遅々として進まず、せめて在学している間に量子アルゴリズムとして最も有名（？）なショアのアルゴリズムだけは理解しようという目標を立てたのですが、なんとこれに2年も費やしてしまいました。頭のいいひとならすぐに理解するのでしょうが…私には無理です。因みにこの勉強には教授から推薦して頂いた、『量子コンピュータ入門』宮野健次郎、古澤明で勉強しました。（英語でよろしければ、量子コンピュータのバイブルとも言えるNielsen and Chungの『Quantum Computation and Quantum Information』に記載されています。Nielsen and Chungの本と他の日本語の本も式の展開は基本的に同じだと思いますが、宮野先生と古澤先生の本は省略無しで丁寧に数式が展開されているので一番わかりやすいと思います。）
余談ですが、何で整数の因数分解にフーリエ変換が出てくるの？と思ったのですが、考えてみれば数字の表記もある周期で桁が上がっていく（もちろん10進数なら10毎に桁上がりする）ので、なるほど各桁の数字というのはパワースペクトルと言ってもよく、数字をフーリエ変換したようなものだと考えるとフーリエ変換が出てくるのも自然だなと思うようになりました。（間違っているかも知れませんがお許し下さい）
このアルゴリズムは要するに図１に書いている通り、位数を求めるのですが、この位数を求めるために量子フーリエ変換を使います。桁数が増えるにつれてこの計算が膨大となりますが、量子フーリエ変換を用いると劇的に速くなるということになります。計算に必要なゲート数で比較すると、古典コンピュータによる高速フーリエ変換（FFT）の場合は、指数オーダー\(O(n2^n )\)となる一方、量子フーリエ変換では入力ビット数の2乗オーダー\(O(n^2 )\)と見積もられ、量子フーリエ変換の方が高速な計算が可能となります。
以下、大まかな流れを、『量子コンピュータ入門』を参考に述べます。言葉の間違いや解釈がおかしい点はいくつもあると思いますがお許し下さい。
フーリエ変換については他の本などを参考にして頂くとして説明は飛ばします。
\(\ket{j}\) の量子離散的フーリエ変換は以下のようにあらわされます。つまり\(j\)という数字に対応した\(\ket{j}\)（正規直交基底ベクトル）をフーリエ変換して\(k\)という数字に対応した\(\ket{k}\)を得るようなイメージです。
$$ \hspace{10pt}\ket{j} \longrightarrow\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^{n-1}}e^{i2\pi jk/2^n}\ket{k} $$
量子ビットで表すために\(j\)を2進数、\(j_1 2^{n-1} + j_2 2^{n-2} +…+j_n 2^0 \)で表し、
\(\hspace{10pt} \ket{j} \ =\ \ket{j_1 j_2 j_3…} \ =\ \ket{j_1\otimes j_2\otimes j_3\otimes…} \)とします。
また、１より小さい数も2進数で表す必要がありますので、2進数の少数を次のように定義します。離散的変換のアルゴリズムは数字を10進で表したり、2進で表したりするので、私は非常に混乱しました。慣れかと思いますが…。
$$\hspace{10pt} 0.j_1 j_2 … j_m \ =\ \frac{j_1}{2^1}\ +\ \frac{j_2}{2^2}\ +\ …\ + \ \frac{j_m}{2^m} $$
基底ベクトル|j⟩は、以下の通り量子離散的フーリエ変換されます。ここまでの\(k\)は十進数です。
$$\hspace{10pt}\ket{j} \longrightarrow\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^{n-1}}e^{i2\pi jk/2^n}\ket{k}$$
これを、以下、２進数で表現し、変形すると以下の通りとなります。式変形がちょっとややこしいです。
2進数の上位の桁から、各桁の数字（0か1）が\(k_1,k_2,\cdots,k_n\)で、各桁について\(\ket{0}+\ket{1}\)を取ると、その全ての組み合わせで十進数の\(\ket{0}から\ket{n}\)となるわけです。
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\sum_{k_1=0}^{1}\sum_{k_2=0}^{1}\cdots\sum_{k_n=0}^{1}e^{i2\pi j(k_1\cdot\ 2^{n-1}+k_2\cdot\ 2^{n-2}+\cdots+k_n\cdot\ 2^0)/2^n}\ket{k_1 k_2 \cdots k_n} $$
以下、ちょっとややこしいですが、さらに変形していきます。
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\sum_{k_1=0}^{1}\sum_{k_2=0}^{1}\cdots
\sum_{k_n=0}^{1}e^{i2\pi j(\frac{k_1}{2^1}+\frac{k_2}{2^2}+\cdots+\frac{k_n}{2^n})}
\ket{k_1\ k_2\cdots\ k_n}$$
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\sum_{k_1=0}^{1}\sum_{k_2=0}^{1}\cdots\sum_{k_n=0}^{1}e^{i2\pi j \frac{k_1}{2^1}}\ket{k_1}\otimes
e^{i2\pi j \frac{k_2}{2^2}}\ket{k_2}\otimes\cdots\otimes e^{i2\pi j \frac{k_1}{2^n}}\ket{k_n}$$
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\left( \ket{0}+e^{i2\pi \frac{j}{2^1}}\ket{1} \right)\otimes\left( \ket{0}+e^{i2\pi \frac{j}{2^2}}\ket{1} \right)\otimes
\cdots\otimes\left( \ket{0}+e^{i2\pi \frac{j}{2^n}}\ket{1} \right)$$
これも変わった表現で最初は理解できなかったのですが、例えば\(0.j_{n-1}j_n\)は小数をそのまま表現していて、小数第一位が\(j_{n-1}\)で小数第二位が\(j_{n}\)ということです。この場合は、数\(j\)を\(2^2\)で割るので、\(j\)を２進数で表した場合の小さいほうの２桁が小数以下になり、整数部分のみを考えると\(e^{i2\pi \frac{j}{2^n}}\)は１となりますので、小数部分のみが残るということです。
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\left( \ket{0}+e^{i2\pi 0.j_n}\ket{1} \right)\otimes\left( \ket{0}+e^{i2\pi 0.j_{n-1} j_n}\ket{1} \right)\otimes
\cdots\otimes\left( \ket{0}+e^{i2\pi 0.j_1 j_2 \cdots j_n}\ket{1} \right)$$

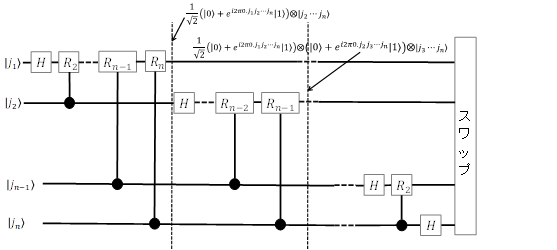
量子フーリエ変換は、図２の回路で実現することができます。因みに制御回転ゲート\(R_m\) は制御ビットが\(\ket{0}\)のときは、標的ビットをそのまま通し、\(\ket{1}\)の時は標的ビットに以下の変換を施すゲートとなります。
$$\ket{0}\longrightarrow\ket{0}\\
\ket{1}\longrightarrow e^{i \frac{2\pi}{2^m}} \ket{1}$$
図の回路に\(\ket{j_1}\ket{j_2}\cdots\ket{j_n}\)を入力して、\(R_2,R_3,\cdots,R_n\)ゲートを通過すると、全体の状態は以下となる。
$$\hspace{10pt}=\frac{1}{\sqrt{2^n}}\left( \ket{0}+e^{i2\pi 0.j_1 j_2 \cdots j_n}\ket{1} \right) \otimes\cdots\otimes\left( \ket{0}+e^{i2\pi 0.j_{n-1} j_n}\ket{1} \right)\otimes\left( \ket{0}+e^{i2\pi 0.j_n}\ket{1} \right)$$
これは量子離散的フーリエ変換の式と逆順になっているため、スワップゲートを通過させることによって、量子離散的フーリエ変換の式と一致することがわかります。

ゲート数で比較すると、高速フーリエ変換の場合は、指数オーダー\(O(n2^n )\)となる一方、量子フーリエ変換では入力ビット数の2乗オーダー\(O(n^2 )\)と見積もられ、量子フーリエ変換の方が高速な計算が可能と言えます。

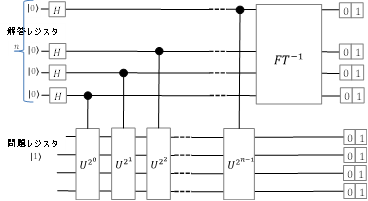
次に位数計算をするための準備として必要な位相推定について述べます。位相推定には先ほど述べた量子離散的フーリエ変換を用います。
位相推定とは、Uをユニタリ演算子として
$$\hspace{10pt} U\ket{u}\ =\ e^{i2\pi \phi}\ket{u}$$
のときに、\(\phi (0\leq \phi <1)\)を求めることです。ここで\(\phi\)を２進数で表し、\(0.\phi_1 \phi_2\cdots\phi_n\)とします。
位相計算をするための回路は図3のように表すことができます。

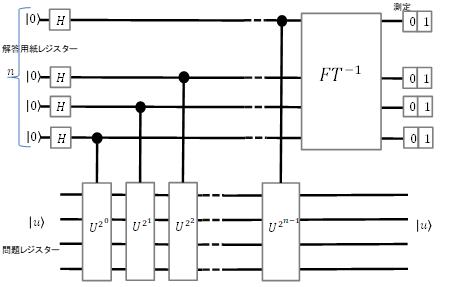
図の回路でアダマール変換を実施したときの状態は
$$\hspace{10pt}\frac{1}{\sqrt{2^n}} (\ket{0}+\ket{1})\otimes (\ket{0}+\ket{1})\otimes\cdots\otimes (\ket{0}+\ket{1})\otimes\ket{u}$$
次に各量子ビットは、制御\(U^{2^k}\)ゲートを通過します。制御\(U^{2^k}\)ゲートは制御ビットが０のときはそのままの値で、制御ビットが1のときは、以下の通り変換するゲートです。
$$\hspace{10pt}\ket{u} \longrightarrow U^{2^k}\ket{u} = e^{i2\pi 2^k \phi}\ket{u}$$
例えば１番目のビットに着目すると、制御\(U^{2^{n-1}}\)ゲートを通過すると
$$\frac{1}{\sqrt{2^n}}(\ket{0}\otimes\cdots\otimes\ket{u}+\ket{1}\otimes\cdots\otimes U^{2^{n-1}}\ket{u} \\
=\frac{1}{\sqrt{2^n}}(\ket{0}\otimes\cdots\otimes\ket{u}+\ket{1}\otimes\cdots\otimes e^{i2\pi 2^{n-1}}\ket{u} \\
=\frac{1}{\sqrt{2^n}}(\ket{0}\otimes\cdots\otimes\ket{u}+e^{i2\pi 2^{n-1}\phi}\ket{1}\otimes\cdots\otimes \ket{u} \\
=\frac{1}{\sqrt{2^n}}\left((\ket{0}+e^{i2\pi 2^{n-1}\phi})\otimes\cdots\otimes\ket{u}\right)$$
従って制御\(U^{2^k}\)ゲートを各量子ビットが通過すると全体の状態は、以下のようになります。
$$\hspace{10pt}\frac{1}{\sqrt{2^n}} (\ket{0} + e^{i2\pi 2^{n-1} \phi}\ket{1})\otimes (\ket{0}+e^{i2\pi 2^{n-2}\phi}\ket{1})\otimes\cdots\otimes (\ket{0}+e^{i2\pi 2^0\phi}\ket{1})\otimes\ket{u}) \\
=\frac{1}{\sqrt{2^n}} (\ket{0} + e^{i2\pi 0.\phi_n}\ket{1})\otimes (\ket{0}+e^{i2\pi 0.\phi_{n-1}\phi_n}\ket{1})\otimes\cdots\otimes (\ket{0}+e^{i2\pi 0.\phi_1\phi_2\cdots\phi_n}\ket{1})\otimes\ket{u}$$

この結果は、\(\ket{\phi_1\phi_2\cdots\phi_n}=\ket{\phi_1}\otimes\ket{\phi_2}\otimes\cdots\otimes\ket{\phi_n}\)を量子フーリエ変換した結果と同じです。
従ってこの式を逆フーリエ変換することにより、\(\ket{\phi_1\phi_2\cdots\phi_n}=\ket{\phi_1}\otimes\ket{\phi_2}\otimes\cdots\otimes\ket{\phi_n}\)を得ることができます。これを測定した結果\(\ket{\phi_1\phi_2\cdots\phi_n}\)を\(2^n\)で割ることで目的の値が得られることになります。
以上により図３の回路で位相推定ができることが確認できました。

このアルゴリズムを10進数表記で表現します。
$$\hspace{10pt}\frac{1}{\sqrt{2^n}}\left(\ket{0}+\ket{1}\right) \otimes \left(\ket{0}+\ket{1}\right) \otimes \cdots \otimes \left(\ket{0}+\ket{1}\right) =\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^{n-1}}\ket{k} $$
なので、制御\(U^{2^k}\)ゲートを各量子ビットが通過すると全体の状態は、
$$\frac{1}{\sqrt{2^n}} \sum_{k_{n-1}=0}^{1} \sum_{k_{n-2}=0}^{1} \cdots \sum_{k_0=0}^{1} \ket{k_{n-1}}\ket{k_{n-2}} \cdots \ket{k_0}
U^{k_{n-1}\cdot 2^{n-1}} U^{k_{n-2}\cdot 2^{n-2}} \cdots U^{k_0 \cdot 2^0} \ket{u} \\
=\frac{1}{\sqrt{2^n}} \sum_{k_{n-1}=0}^{1} \sum_{k_{n-2}=0}^{1} \cdots \sum_{k_0=0}^{1} \ket{k_{n-1} k_{n-2} \cdots k_0}
U^{k_{n-1}\cdot 2^{n-1}+k_{n-2}\cdot 2^{n-2}+ \cdots + k_0 \cdot 2^0} \ket{u} \\
=\frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} \ket{k} \otimes U^k \ket{u} $$
となります。さらに変形すると、
$$=\frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} \ket{k} \otimes e^{i2 \pi k \phi} \ket{u} \\
=\frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{i2 \pi k \phi} \ket{k} \otimes \ket{u} \\
=\frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{\frac{i2 \pi k \tilde{\phi}}{2^n}} \ket{k} \otimes \ket{u} \\
=\frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{i2 \pi \tilde{\phi} k}{N}} \ket{k} \otimes \ket{u} $$
但し、\(0.\phi_1\phi_2\cdots \phi_n\)、\(\tilde{\phi}=2^n\phi=\phi_1\phi_2\cdots \phi_n \)を用いた。

次は位相計算です。正の整数nと互いに素な、n未満の正整数の集合\(G={a|1≤x<M,gcd⁡(x,M)=1}\)の任意のx∈Gに対して\(x^r mod M=1\)　を満たす正整数rがつねに存在します。
rをxのmod Mに関する位数（order）と呼び、order(x)で表します。古典的なコンピュータで位数rを計算することは難しい問題であると言われています。
\(U\ket{y}\equiv\ket{xy\ mod\ M}\)を満たす\(U\)、固有ベクトル\(\ket{u_s}\)、固有値\(e^{i2\pi\frac{s}{r}}\ (s=0,1,2,\cdots,r-1)\)を求めます。つまり\(U\ket{u_s}=e^{i2\pi\frac{s}{r}}\ket{u_s}\)において位相推定問題を解くことになります。（\(\frac{s}{r}\)が求める値となります。）
ここで、\(\ket{u_s}\)は
$$\hspace{10pt} \ket{u_s}=\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-i2\pi j\frac{r}{s}}\ket{x^j \ mod\ M}$$
ここで、\(x^j \ mod \ M=q\)とすると、\(x^j = pM+q\)と書くことができます。（\(p,q\)は自然数）そうすると、
$$\hspace{10pt} U\ket{x^j\ mod\ M}=\ket{x(pM+q)\ mod \ M}=xq \ mod\ M $$
$$\hspace{10pt}\ket{x^{j+1}\ mod\ M}=\ket{x\cdot x^j\ mod\ M}=\ket{x(pM\ +\ q)mod\ M}=xq\ mod\ M$$
となりますので、これを用いると\(U\ket{u_s}\)は
$$\hspace{10pt}U\ket{u_s}=U\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-i2\pi j\frac{s}{r}}\ket{x^j \ mod\ M}=\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-i2\pi j\frac{s}{r}}\ket{x^{j+1} \ mod\ M}$$
$$\hspace{20pt}=\frac{1}{\sqrt{r}} \left( e^{-i2\pi\cdot 0\frac{s}{r}}\ket{x^1 \ mod\ M}+e^{-i2\pi\cdot 1\frac{s}{r}}\ket{x^2 \ mod\ M}+\cdots+e^{-i2\pi\cdot (r-1)\frac{s}{r}}\ket{x^r \ mod\ M}\right)$$
$$\hspace{20pt}= e^{i2 \pi \frac{s}{r}}\frac{1}{\sqrt{r}} \left( e^{-i2 \pi \cdot 1 \cdot \frac{s}{r}}\ket{x^{1} \ mod\ M}+e^{-i2 \pi \cdot 2 \cdot \frac{s}{r}}\ket{x^{2} \ mod\ M}+\cdots +e^{-i2 \pi \cdot r \cdot \frac{s}{r}}\ket{1 \ mod\ M} \right) $$
$$\hspace{20pt}= e^{i2 \pi \frac{s}{r}}\frac{1}{\sqrt{r}} (e^{-i2 \pi \cdot 0 \cdot \frac{s}{r}}\ket{x^{0} \ mod\ M}+ e^{-i2 \pi \cdot 1 \cdot \frac{s}{r}}\ket{x^{1} \ mod\ M}+e^{-i2 \pi \cdot 2 \cdot \frac{s}{r}}\ket{x^{2} \ mod\ M} \ +\cdots +e^{-i2 \pi \cdot (r-1) \cdot \frac{s}{r}}\ket{x^{r-1} \ mod\ M} ) $$
$$\hspace{20pt}= e^{i2 \pi \frac{s}{r}}\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1} e^{-i2 \pi j \frac{s}{r}}\ket{x^j \ mod\ M} $$
$$\hspace{20pt}= e^{i2 \pi \frac{s}{r}}\ket{u_s} $$
従って、以下の式が成り立ちます。
$$\hspace{20pt}U\ket{u_s}=e^{i2\pi j\frac{s}{r}}$$
一方、
$$\hspace{20pt}\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s} = \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1} \frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}\ket{x^j \ mod\ M}$$
$$\hspace{60pt}=\frac{1}{r}\sum_{j=0}^{r-1}\left( \sum_{s=0}^{r-1} e^{i2\pi j\frac{s}{r}}\right) \ket{x^j \ mod\ M}$$
ここで、（）内は、\(j=0\)のときは\(r\)、\(j\neq 0\)のときは\(0\)となりますので、
$$\hspace{60pt}=\frac{1}{r}r\ket{x^0 \ mod\ M} = \ket{1}$$
となりますので以下が成り立ちます。
$$\hspace{20pt}\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}= \ket{1}$$
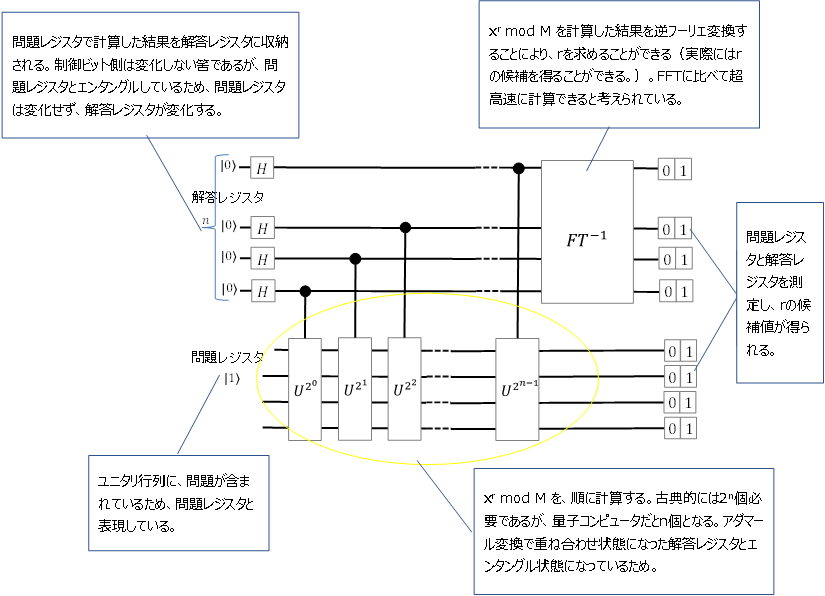
図3の量子回路の\(\ket{u_s}\)の代わりに\(\ket{1}\)を入力すると、図４のようになり、

全体の状態は、
$$\hspace{60pt}\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\ket{1}$$
となりますので、以下の通り変形することができます。
$$\hspace{60pt}\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\ket{1}=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}$$
$$\hspace{60pt}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\ket{u_s}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes e^{i2\pi k\frac{s}{r}}\ket{u_s}$$
$$\hspace{60pt}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left( \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} e^{i2\pi k\frac{s}{r}}\ket{k}\right) \otimes\ket{u_s}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left( \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} e^\frac{{i2\pi k\frac{\tilde{s}}{r}}}{2^n}\ket{k}\right) \otimes\ket{u_s}$$
$$\hspace{60pt}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\left( \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} e^\frac{{i2\pi k\frac{\tilde{s}}{r}}}{N}\ket{k}\right) \otimes\ket{u_s}$$
但し、以下を用いています。
$$\hspace{60pt}\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}= \ket{1}、U\ket{u_s}=e^{i2\pi \frac{s}{r}}\ket{u_s}、\frac{\tilde{s}}{r}=2^n\frac{s}{r}、2^n=N$$
つまり、図３の解答レジスタは、\(0\)から\(r-1\)までの\(r\)通りの\(s\)を持つ状態
$$\hspace{60pt}\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} e^\frac{{i2\pi k\frac{\tilde{s}}{r}}}{N}\ket{k}$$
の重ね合わせになっていることがわかります。
制御\(U^{2^k}\)ゲートは、\(k\)を\(0\)から\(N\)までの場合について\(x^k \ mod\ M\)を計算した重ね合わせを行っていることになります。制御\(U^{2^0}\cdots U^{2^{n-1}}\)ゲートを通過した後、問題レジスタを測定し、解答レジスタを逆量子フーリエ変換すると求める位数\(r\)が\(x^r\ mod\ M=1\)を満たしますから、解答レジスタに\(r\)の周期で係数の絶対値の２乗がゼロより十分大きい\(\ket{k}\)が現れ、目的の\(r\)を求めることができます。素因数分解をしたい\(M\)について\((x,r)\)の組を求めるのが目的なのですが、\(r\)の周期が大き過ぎる場合に\(r\)を求められない場合は、\(x\)を選びなおすことになります。
ということで、位数\(r\)が確定できれば図1の手順で因数分解ができることになります。それにしてもこの複雑なアルゴリズムの実装は可能なのでしょうか？2001年にIBMがショアのアルゴリズムを用いて15の因数分解（=3×5）に成功したそうで、その後も桁数が増えているにせよ、暗号に使うような桁数の量子コンピュータはすぐに実現しそうにないように思えます。当然ながら正確な計算をしなければいけないのですが、量子コンピュータの誤り訂正はは古典コンピュータの誤り訂正（パリティチェックなど）のように簡単にはいかないそうです。つまり量子情報はコピーができませんので、古典コンピュータのようにビット情報をコピーして冗長化をすることができません。量子ビットの誤り訂正方法はいくつもの提案があるそうですが、一説によると実現するためには、\(10^4\)から\(10^5\)倍の量子ビットが必要であるとも言われているそうです。まだかなりの時間がかかるのではないでしょうか。

【ショアのアルゴリズムの追加説明１】
　ショアのアルゴリズムについて自分なりに理解したことをアルゴリズム回路に大雑把に書いてみました。

【ショアのアルゴリズムの追加説明２】
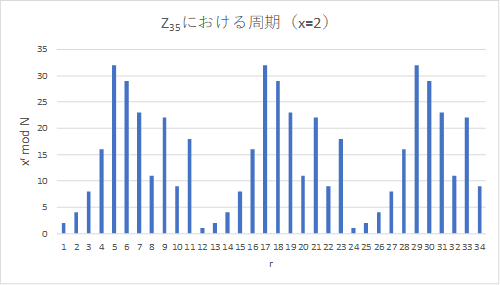
　簡単な例（M=35の因数分解）
位数を量子コンピュータで計算し、位数から、因数を求める。
適当な数、\(X\)を2とする。 \(x^r\ mod\ M\) をrを1から順に計算すると下図のグラフになる。
これから周期\(r\ （x^r\ mod\ M = 1\)となる\(ｒ)\)は12となる。
⇒このｒを量子フーリエ変換で計算する。

偶数となるｒが見つかれば
\((x^r -1) = (26 -1) (26 +1) = (23 -1) (23 +1)(26 +1) = 7×9×65\)となり、因数7が得られる。
※量子コンピュータ研究における実験では、ショアのアルゴリズムを用いて、この程度の大きさの数字の因数分解が多く行われている。（今のところ、暗号解読ができるビット数を持つ量子コンピュータは実現困難）