基本的な量子ゲート
$$ \def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} $$
従来のコンピュータ(古典コンピュータ)は、情報の基本単位を「ビット(bit: binary digit)」とし、「0」と「1」のいずれか一方の状態を取ることで、2進数により演算し、情報の保存と処理を行います。この状態は、例えば「0」を電圧0V、「1」を電圧5Vに対応づけることにより実現されます。
一方、量子コンピュータでは「量子ビット(qubit: quantum bit)」とよばれる情報単位を用います。量子ビットは重ね合わせ(superposition)により「0」と「1」の両方の状態を取ることができます。これは古典コンピュータのビットで、「0」と「1」の間の電圧2.5Vの状態を取るというのとは根本的に異なります。
通常のビットの「0」と「1」に対応する量子ビットは、量子力学で良く用いられるブラケット記号\(\ket{0}\)または\(\ket{1}\)(これはブラケット表記のケット記号)で表されます。
量子ビットの状態は、図1のようにブロッホ球と呼ばれる球面の1点で表すことができます。ブロッホ球を用いて、図2のように北極点\((x,y,z)=(0,0,1)\)を\(\ket{0}\)、南極点\((x,y,z)=(0,0,-1)\)を\(\ket{1}\)に対応させています。
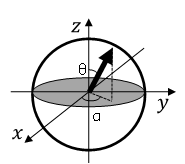
図1
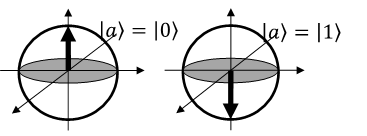
例えば、\(\ket{0}\)をy軸の周りに回転させることにより、図3のように\(\ket{0}\)と\(\ket{1}\)の重ね合わせ状態となります。
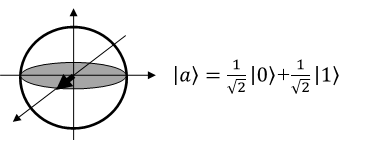
ブロッホ球内での回転は、次の式で表されます。
$$c_0\ket{0} + c_1\ket{1} \longrightarrow\ c’_0\ket{0} + c’_1\ket{1} $$
\(\ket{0} と \ket{1}\)はベクトル形式では次のように表されます(大きさ1で、互いに直交する直交基底ベクトル)。
$$\ket{0} = \left[\begin{array}{c}1\\0 \end{array}\right] 、\ket{1} = \left[\begin{array}{c}0\\1 \end{array}\right]$$
これをユニタリ行列\(U\)と呼ばれる変換を行うと
$$U \left[\begin{array}{c}c_0 \\c_1 \end{array}\right] = \left[\begin{array}{c}c’_0 \\c’_1 \end{array}\right] $$
ここで、\(c_0 ,c_1 ,c’_0 ,c’_1\)は複素数です。\(U\)は1qbitに対する演算を行う行列でブロッホ球内での回転を表し、量子回路ではユニタリゲートと呼ばれ、以下の表現が用いられます。

1qbitの代表的な演算としてパウリゲート(Pauli gates)が用いられます。行列で表すと
$$X = \left[\begin{array}{cc}0 & 1 \\1 & 0 \end{array}\right] ,Y = \left[\begin{array}{cc}0 & -i \\i & 0 \end{array}\right] ,Z = \left[\begin{array}{cc}1 & 0 \\0 & -1 \end{array}\right]$$
パウリゲートXは反転演算、パウリゲートZは位相反転演算となります。


またよく用いられるユニタリゲートとしてウォルシュ・アダマールゲート(上記の図3)があります。
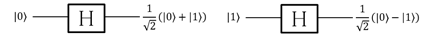
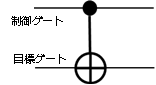
2qbitに対する演算を行う量子ゲートとしてよく用いられるCNOTゲート(Controlled-NOT gate)があります。これは、制御ゲートが0の場合は、目標ゲートに何も作用せず、制御ゲートが1の場合は、NOT演算を行うゲートです。
古典的な論理回路において、どのような論理回路も構成できるゲート(universal gate:万能ゲート)として知られているものとしてNANDゲートがあります。
これと同様にユニタリゲートとCNOTゲートは、量子ゲートにおけるユニバーサルゲートとなります。